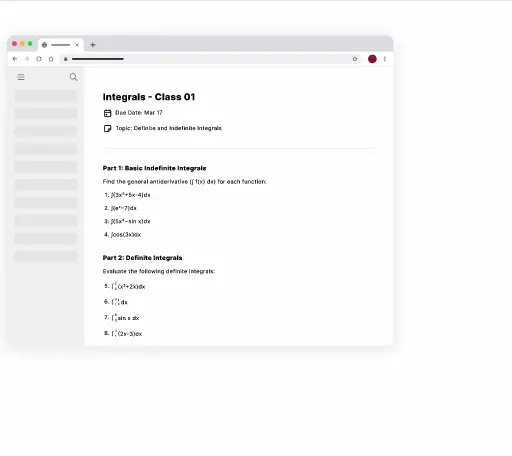
Summary: The Coordinate Plane
Key Concepts
- Ordered Pair An ordered pair, gives the coordinates of a point in a rectangular coordinate system.
- Steps for Plotting an Ordered Pair (x, y) in the Coordinate Plane
- Determine the x-coordinate. Beginning at the origin, move horizontally, the direction of the x-axis, the distance given by the x-coordinate. If the x-coordinate is positive, move to the right; if the x-coordinate is negative, move to the left.
- Determine the y-coordinate. Beginning at the x-coordinate, move vertically, the direction of the y-axis, the distance given by the y-coordinate. If the y-coordinate is positive, move up; if the y-coordinate is negative, move down.
- Draw a point at the ending location. Label the point with the ordered pair.
- An ordered pair is represented by a single point on the graph.
- Sign Patterns of the Quadrants
Quadrant I Quadrant II Quadrant III Quadrant IV - Coordinates of Zero
- Points with a -coordinate equal to are on the x-axis, and have coordinates .
- Points with a -coordinate equal to are on the y-axis, and have coordinates .
- The point is called the origin. It is the point where the x-axis and y-axis intersect.
-
Identifying Solutions To find out whether an ordered pair is a solution of a linear equation, you can do the following:
- Graph the linear equation, and graph the ordered pair. If the ordered pair appears to be on the graph of a line, then it is a possible solution of the linear equation. If the ordered pair does not lie on the graph of a line, then it is not a solution.
- Substitute the (x, y) values into the equation. If the equation yields a true statement, then the ordered pair is a solution of the linear equation. If the ordered pair does not yield a true statement then it is not a solution.
Glossary
- linear equation
- An equation of the form , where and are not both zero, is called a linear equation in two variables.
- ordered pair
- An ordered pair gives the coordinates of a point in a rectangular coordinate system. The first number is the -coordinate. The second number is the -coordinate.
- origin
- The point is called the origin. It is the point where the the point where the -axis and -axis intersect.
- quadrants
- The -axis and -axis divide a rectangular coordinate system into four areas, called quadrants. The quadrants are labeled with the Roman Numerals I, II, III, IV going around the coordinate system in a counter-clockwise direction.
- solution to a linear equation in two variables
- An ordered pair is a solution to the linear equation , if the equation is a true statement when the x- and y-values of the ordered pair are substituted into the equation.
- x-axis
- The x-axis is the horizontal axis in a rectangular coordinate system.
- y-axis
- The y-axis is the vertical axis on a rectangular coordinate system.
Contribute!
Did you have an idea for improving this content? We’d love your input.