Finding the Product of Two Matrices
In addition to multiplying a matrix by a scalar, we can multiply two matrices. Finding the product of two matrices is only possible when the inner dimensions are the same, meaning that the number of columns of the first matrix is equal to the number of rows of the second matrix. If is an matrix and is an matrix, then the product matrix is an matrix. For example, the product is possible because the number of columns in is the same as the number of rows in . If the inner dimensions do not match, the product is not defined.
 Figure 1
Figure 1
Multiply and add as follows to obtain the first entry of the product matrix .
- To obtain the entry in row 1, column 1 of multiply the first row in by the first column in , and add.
- To obtain the entry in row 1, column 2 of multiply the first row of by the second column in , and add.
- To obtain the entry in row 1, column 3 of multiply the first row of by the third column in , and add.
A General Note: Properties of Matrix Multiplication
For the matrices and the following properties hold.- Matrix multiplication is associative: .
- Matrix multiplication is distributive:
Example 8: Multiplying Two Matrices
Multiply matrix and matrix .Solution
First, we check the dimensions of the matrices. Matrix has dimensions and matrix has dimensions . The inner dimensions are the same so we can perform the multiplication. The product will have the dimensions . We perform the operations outlined previously.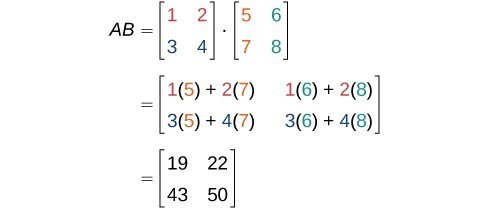 Figure 2
Figure 2Example 9: Multiplying Two Matrices
Given and- Find .
- Find .
Solution
- As the dimensions of are and the dimensions of are these matrices can be multiplied together because the number of columns in matches the number of rows in . The resulting product will be a matrix, the number of rows in by the number of columns in .
- The dimensions of are and the dimensions of are . The inner dimensions match so the product is defined and will be a matrix.
Analysis of the Solution
Notice that the products and are not equal.
This illustrates the fact that matrix multiplication is not commutative.
Q & A
Is it possible for AB to be defined but not BA?
Yes, consider a matrix A with dimension and matrix B with dimension . For the product AB the inner dimensions are 4 and the product is defined, but for the product BA the inner dimensions are 2 and 3 so the product is undefined.Example 10: Using Matrices in Real-World Problems
Let’s return to the problem presented at the opening of this section. We have the table below, representing the equipment needs of two soccer teams.| Wildcats | Mud Cats | |
|---|---|---|
| Goals | 6 | 10 |
| Balls | 30 | 24 |
| Jerseys | 14 | 20 |
| Goal | $300 |
| Ball | $10 |
| Jersey | $30 |
The cost matrix is written as
We perform matrix multiplication to obtain costs for the equipment.
The total cost for equipment for the Wildcats is $2,520, and the total cost for equipment for the Mud Cats is $3,840.
How To: Given a matrix operation, evaluate using a calculator.
- Save each matrix as a matrix variable .
- Enter the operation into the calculator, calling up each matrix variable as needed.
- If the operation is defined, the calculator will present the solution matrix; if the operation is undefined, it will display an error message.
Example 11: Using a Calculator to Perform Matrix Operations
Find given.
Solution
On the matrix page of the calculator, we enter matrix above as the matrix variable , matrix above as the matrix variable , and matrix above as the matrix variable . On the home screen of the calculator, we type in the problem and call up each matrix variable as needed.
The calculator gives us the following matrix.
