Solutions
Solutions to Try Its
1. ∣x−2∣≤3
2. using the variable p for passing, ∣p−80∣≤20
3. f(x)=−∣x+2∣+3
4. x=−1 or x=2
5. f(0)=1, so the graph intersects the vertical axis at (0,1). f(x)=0 when x=−5 and x=1 so the graph intersects the horizontal axis at (−5,0) and (1,0).
6. 4≤x≤8
7. k≤1 or k≥7; in interval notation, this would be (−∞,1]∪[7,∞)
Solutions to Odd-Numbered Exercises
1. Isolate the absolute value term so that the equation is of the form ∣A∣=B. Form one equation by setting the expression inside the absolute value symbol, A, equal to the expression on the other side of the equation, B. Form a second equation by setting A equal to the opposite of the expression on the other side of the equation, -B. Solve each equation for the variable.
3. The graph of the absolute value function does not cross the x -axis, so the graph is either completely above or completely below the x -axis.
5. First determine the boundary points by finding the solution(s) of the equation. Use the boundary points to form possible solution intervals. Choose a test value in each interval to determine which values satisfy the inequality.
7. ∣x+4∣=21
9. ∣f(x)−8∣<0.03
11. {1,11}
13. {49,413}
15. {310,320}
17. {511,529}
19. {25,27}
21. No solution
23. {−57,27}
25. (0,−8);(−6,0),(4,0)
27. (0,−7); no x -intercepts
29. (−∞,−8)∪(12,∞)
31. 3−4≤x≤4
33. (−∞,−38]∪[6,∞)
35. (−∞,−38]∪[16,∞)
37.
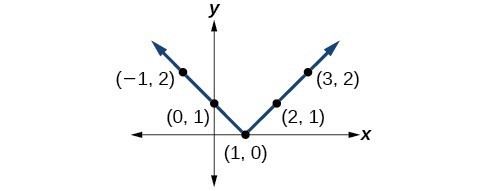 39.
39.
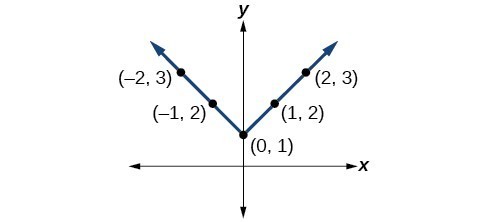 41.
41.
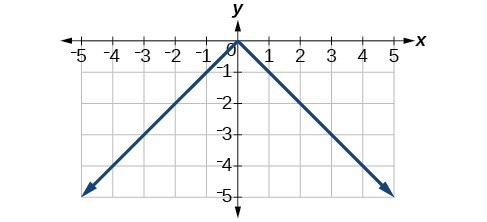 43.
43.
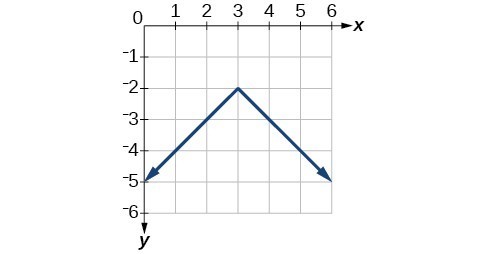 45.
45.
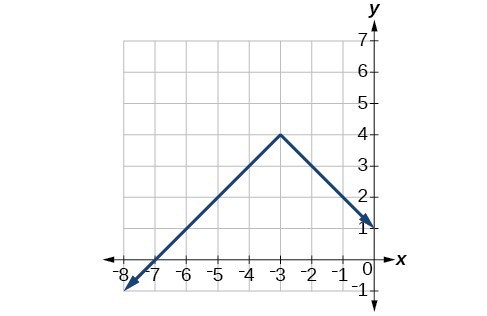 47.
47.
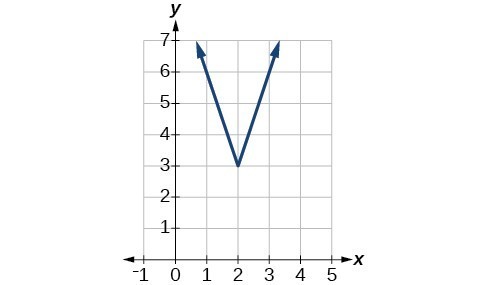 49.
49.
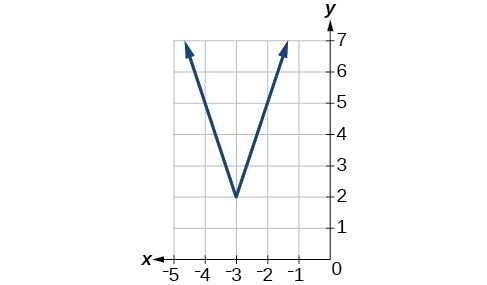 51.
51.
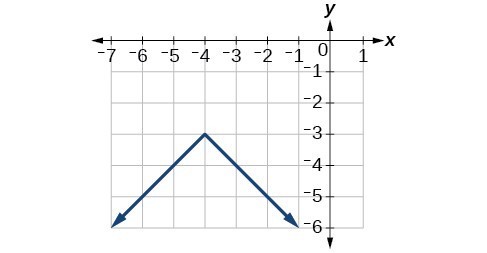 53. range: [0,20]
53. range: [0,20]
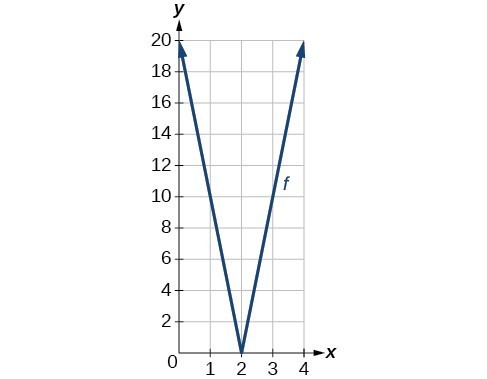 55. x- intercepts:
55. x- intercepts:
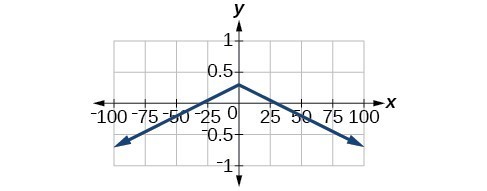 57. (−∞,∞)
59. There is no solution for a that will keep the function from having a y -intercept. The absolute value function always crosses the y -intercept when x=0.
61. ∣p−0.08∣≤0.015
63. ∣x−5.0∣≤0.01
57. (−∞,∞)
59. There is no solution for a that will keep the function from having a y -intercept. The absolute value function always crosses the y -intercept when x=0.
61. ∣p−0.08∣≤0.015
63. ∣x−5.0∣≤0.01Licenses & Attributions
CC licensed content, Shared previously
- Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download For Free at : http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175..
 39.
39.
 41.
41.
 43.
43.
 45.
45.
 47.
47.
 49.
49.
 51.
51.
 53. range:
53. range:
 55. intercepts:
55. intercepts:
 57.
59. There is no solution for that will keep the function from having a -intercept. The absolute value function always crosses the -intercept when .
61.
63.
57.
59. There is no solution for that will keep the function from having a -intercept. The absolute value function always crosses the -intercept when .
61.
63. 