Solutions
Solutions to Try Its
1. (2,∞)
2. (5,∞)
3. The domain is (0,∞), the range is (−∞,∞), and the vertical asymptote is x = 0.
 4. The domain is (−4,∞), the range (−∞,∞), and the asymptote x = –4.
4. The domain is (−4,∞), the range (−∞,∞), and the asymptote x = –4.
 5. The domain is (0,∞), the range is (−∞,∞), and the vertical asymptote is x = 0.
5. The domain is (0,∞), the range is (−∞,∞), and the vertical asymptote is x = 0.
 6. The domain is (0,∞), the range is (−∞,∞), and the vertical asymptote is x = 0.
6. The domain is (0,∞), the range is (−∞,∞), and the vertical asymptote is x = 0.
 7. The domain is (2,∞), the range is (−∞,∞), and the vertical asymptote is x = 2.
8. The domain is (−∞,0), the range is (−∞,∞), and the vertical asymptote is x = 0.
7. The domain is (2,∞), the range is (−∞,∞), and the vertical asymptote is x = 2.
8. The domain is (−∞,0), the range is (−∞,∞), and the vertical asymptote is x = 0.

9. x≈3.049
10. x = 1
11. f(x)=2ln(x+3)−1
Solutions to Odd-Numbered Exercises
1. Since the functions are inverses, their graphs are mirror images about the line y = x. So for every point (a,b) on the graph of a logarithmic function, there is a corresponding point (b,a) on the graph of its inverse exponential function.
3. Shifting the function right or left and reflecting the function about the y-axis will affect its domain.
5. No. A horizontal asymptote would suggest a limit on the range, and the range of any logarithmic function in general form is all real numbers.
7. Domain: (−∞,21); Range: (−∞,∞)
9. Domain: (−417,∞); Range: (−∞,∞)
11. Domain: (5,∞); Vertical asymptote: x = 5
13. Domain: (−31,∞); Vertical asymptote: x=−31
15. Domain: (−3,∞); Vertical asymptote: x = –3
17. Domain: (73,∞); Vertical asymptote: x=73 ; End behavior: as x→(73)+,f(x)→−∞ and as x→∞,f(x)→∞
19. Domain: (−3,∞) ; Vertical asymptote: x = –3; End behavior: as x→−3+ , f(x)→−∞ and as x→∞ , f(x)→∞
21. Domain: (1,∞); Range: (−∞,∞); Vertical asymptote: x = 1; x-intercept: (45,0); y-intercept: DNE
23. Domain: (−∞,0); Range: (−∞,∞); Vertical asymptote: x = 0; x-intercept: (−e2,0); y-intercept: DNE
25. Domain: (0,∞); Range: (−∞,∞); Vertical asymptote: x = 0; x-intercept: (e3,0); y-intercept: DNE
27. B
29. C
31. B
33. C
35.
 37.
37.
 39. C
41.
39. C
41.
 43.
43.
 45.
45.
 47. f(x)=log2(−(x−1))
49. f(x)=3log4(x+2)
51. x = 2
53. x≈2.303
55. x≈−0.472
57. The graphs of f(x)=log21(x) and g(x)=−log2(x) appear to be the same; Conjecture: for any positive base b=1, logb(x)=−logb1(x).
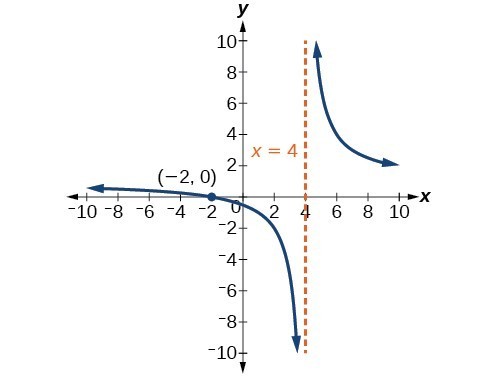
59. Recall that the argument of a logarithmic function must be positive, so we determine where x−4x+2>0 . From the graph of the function f(x)=x−4x+2, note that the graph lies above the x-axis on the interval (−∞,−2) and again to the right of the vertical asymptote, that is (4,∞). Therefore, the domain is (−∞,−2)∪(4,∞).
47. f(x)=log2(−(x−1))
49. f(x)=3log4(x+2)
51. x = 2
53. x≈2.303
55. x≈−0.472
57. The graphs of f(x)=log21(x) and g(x)=−log2(x) appear to be the same; Conjecture: for any positive base b=1, logb(x)=−logb1(x).
59. Recall that the argument of a logarithmic function must be positive, so we determine where x−4x+2>0 . From the graph of the function f(x)=x−4x+2, note that the graph lies above the x-axis on the interval (−∞,−2) and again to the right of the vertical asymptote, that is (4,∞). Therefore, the domain is (−∞,−2)∪(4,∞).
Licenses & Attributions
CC licensed content, Shared previously
- Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download For Free at : http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175..
 4. The domain is , the range , and the asymptote x = –4.
4. The domain is , the range , and the asymptote x = –4.
 5. The domain is , the range is , and the vertical asymptote is x = 0.
5. The domain is , the range is , and the vertical asymptote is x = 0.
 6. The domain is , the range is , and the vertical asymptote is x = 0.
6. The domain is , the range is , and the vertical asymptote is x = 0.
 7. The domain is , the range is , and the vertical asymptote is x = 2.
7. The domain is , the range is , and the vertical asymptote is x = 2.


 37.
37.
 39. C
41.
39. C
41.
 43.
43.
 45.
45.
 47.
49.
51. x = 2
53.
55.
57. The graphs of and appear to be the same; Conjecture: for any positive base , .
59. Recall that the argument of a logarithmic function must be positive, so we determine where . From the graph of the function , note that the graph lies above the x-axis on the interval and again to the right of the vertical asymptote, that is . Therefore, the domain is .
47.
49.
51. x = 2
53.
55.
57. The graphs of and appear to be the same; Conjecture: for any positive base , .
59. Recall that the argument of a logarithmic function must be positive, so we determine where . From the graph of the function , note that the graph lies above the x-axis on the interval and again to the right of the vertical asymptote, that is . Therefore, the domain is .